The First Black Jack Game - Mowin People Games

This post is about my experience creating a script to analyze the probabilities of a game. You can see it on my GitHub here.

Something For Euchre Players to get Mad About

If you’ve ever played the card game Euchre, you may be familiar with the small game of luck which is used to determine the first player to deal. The game is very simple, cards are passed out to players one at a time going clockwise. Whoever gets the first black jack wins the game and gets to be the first dealer in Euchre. I call this game the ‘First Black Jack Game’.

There are 4 players in Euchre on 2 teams and partners sit opposite each. The game is played with 24 cards 2 of which are black jacks. And to be clear, getting the deal is a good thing.

But, let me ask you this, is this game fair? It feels pretty fair, but that’s not good enough! We must know for sure. If you are mathematically inclined, now is the time to try and prove if the game described above is biased, and if so which team it is biased towards. (It helps to describe the team that is dealt a card first as Team 1 and the other team as Team 2).

The Math

This game is very easy to generalize with 3 parameters:

C = total number of cards in the deck
J = number of black jacks (winning cards) in the deck
T = number of teams

In the typical Euchre version of this game, C=24, J=2, and T=2 (or 4 if you care about which partner gets the deal).

It’s always a good idea to start at a simple case to get a feel for a problem. Consider the game with 4 cards in the deck (C=4), 2 black jacks (J=2), and 2 teams (T=2).

Let Team 1 or T1 denote the first team that is dealt a card, and Team 2 the second.

In this game, the probability that card 1 is the first black jack denoted P(C1 is first J) is the number of jacks over the number of total cards, or 2/4 = 50%, so it seems likely that this game is biased towards team 1.

We can create a probability tree for this game where each step we see if another card is a black jack or not. Once a black jack is found, the game stops, so tree only continues when a card is found not to be a black jack.

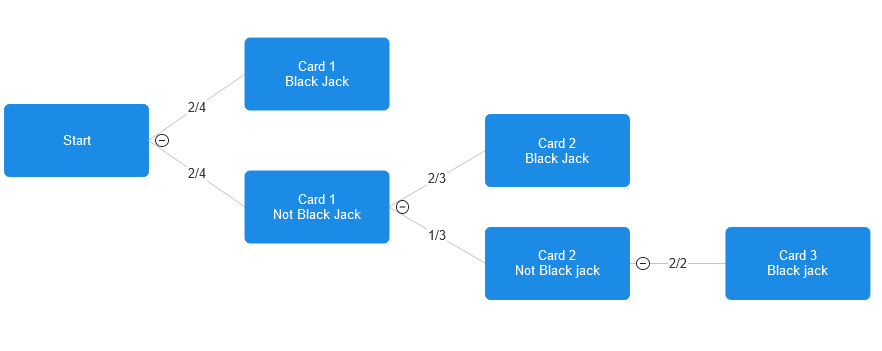
After Card 1 is found to not be a black jack, there are 3 cards left in the deck and 2 black jacks, so the probability that card 2 is found to be a black jack at this point is 2/3 as seen in the tree above.

To find the probability of any card being the first black jack, we just multiply the values on the lines following the path from the start to our wanted end point. Thus,

P(C1 is first J) $= \frac{2}{4} = \frac{1}{2}$

P(C2 is first J) $= \frac{2}{4}\frac{2}{3} = \frac{1}{3}$

P(C3 is first J) $= \frac{2}{4}\frac{2}{3}\frac{2}{2} = \frac{1}{6}$

Notice that P(C4 is first J) = 0 bnecause there are two black jacks, so there is no way for the final card to be the first black jack.

Team 1 gets cards 1 and 3 while Team 2 gets 2 and 4, so

P(Team 1 wins) = P(C1 is first J) + P(C3 is first J) = $\frac{2}{3}$

P(Team 2 wins) = P(C2 is first J) + P(C4 is first J) = $\frac{1}{3}$

So as we predicted, Team 1 has a large advantage in this game. By understanding the process we just undertook, we can create an algorithm to calculate the probability of a team winning for any game.

Creating an Algorithm

Here is a probability tree for the game with 6 cards in the deck, 2 of which are black jacks:

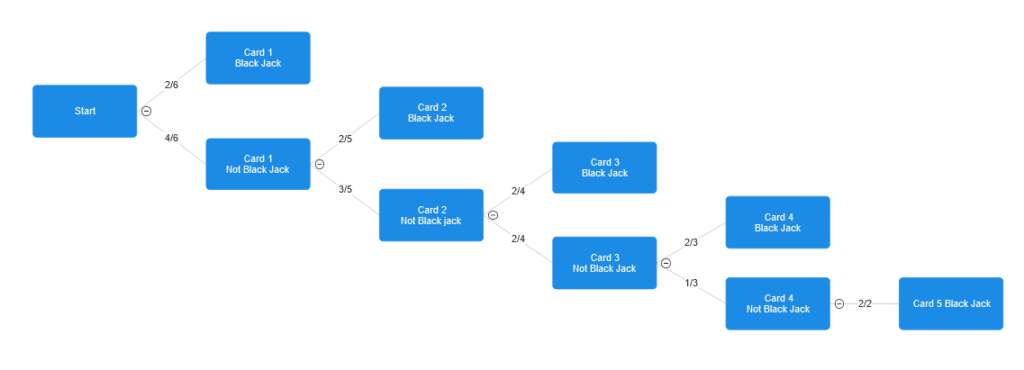
To calculate the probability of a team winning, we just have to add up the probabilities that their cards are the first black jack. The hard part is getting a general expression for P(Cv is first J) for some integer v.

What is easy is calculating P(C1 is first J). This is just the number of black jacks divided by the number of cards. In this case, it is 2/6 = 1/3. For a game where there are c total cards and j black jacks, let’s say P(C1 is first J) = $p(c,j) = \frac{j}{c}$ .

Also, define $q(c,j) = 1-p(c,j) = \frac{c-j}{c}$ .

Now, each time a card is revealed not to be a black jack, the deck loses a card, but the number of jacks stays the same, so the probability that the second card will be a jack is $\frac{j}{c-1} = p(c-1,j)$ .

As we see in the picture, the deck shrinks from 6 to 5 cards, but there are still 2 black jacks, so we get 2/5 on the branch from card 1 not a black jack to card 2 black jack.

We can generalize this for any integer v. Given that all previous cards were not black jacks, the probability that Card v is a black jack is $p(c-v+1,j)$ .

Here is a probability table for any First Black Jack Game:

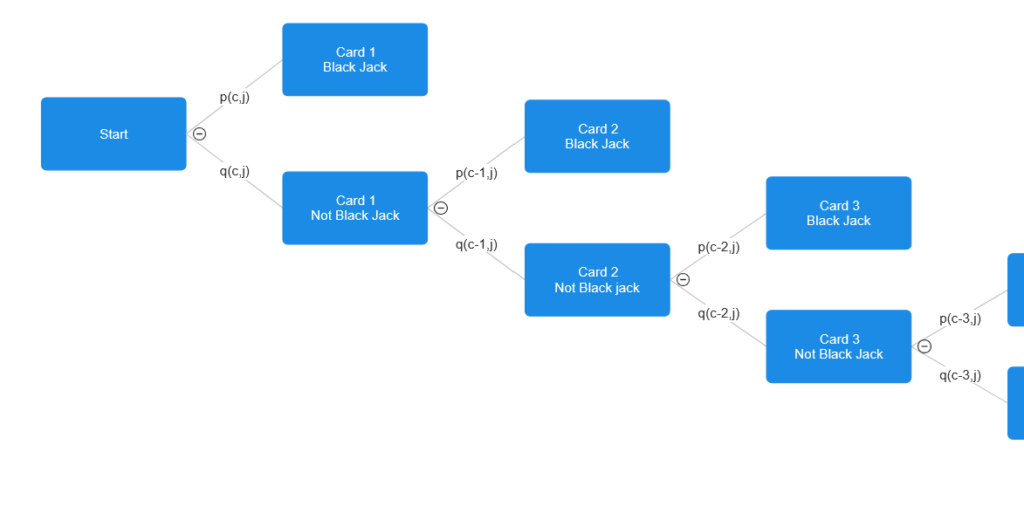
To calculate P(Cv is first J), we just calculate the product down the tree to the wanted leaf. Thus,

P(Cv is first J) = $q(c,j)q(c-1,j)q(c-2,j)...q(c-v+2,j)p(c-v+1,j)$

Note

The above equation only works for cards that have a path on the probability tree from start, that is the cards with nonzero probability of being the first black jack.

Assuming that there are j black jacks and c cards, if $v>c-j+1$ , then it is impossible for a jack not to be pulled before card v, so P(Cv is first J) = 0.

If $v\leq c-j+1$ , then we can use the equation above.

Now, we can create an algorithm to calculate the probability of a team winning.

First, based on the number of teams, we can figure out which cards that team will get. Then, we calculate and add up P(Cv is first J) for each of their cards to get the probability of that team winning. This is exactly how my original script worked.

P(Team 1 wins) = P(C1 is first J) + P(C(1+T) is first J) + …

Results

For the Euchre version of the game, the team win probabilities are calculated out to be:

P(Team 1 wins) = 52.1739%

P(Team 2 wins) = 47.8261%

So, the first team has a slight advantage in this game. If you’re ever feeling butthurt from a game of Euchre, go ahead and pull this statistic to explain your loss away. Or if you want to be that guy, tell the dealer to only make the Jack of Spades a winning card. This will make the odds even for both teams.

Optimizing the Code

The algorithm described above is good enough for any reasonable person. It calculates the team winning probabilities for the Euchre version of the game in no time flat. But, this was coded in C++, so everything must be sacrificed for speed!

The old algorithm showed some signs of slowing when you inputted a deck of 10000 cards or so. For the game C=10000, J=1000, and T=10, the old program took 1333 milliseconds. Unacceptable! The old algorithm can be improved upon greatly.

To be more descriptive, the old algorithm did this:

For each team:
1. Find the card numbers that belong to this team
2. Create a variable to store the total win probability
3. For each card number v:
  1. Create a variable to store the running product (this will be P(Cv is first J))
  2. For each card number w from c to c-v+2:
    1. Calculate q(w,j) and multiply it to the running product
  3. Multiply p(c-v+1,j) to the running product
  4. Add the running product to the total win probability
  5. Print out the win probability for this team

But realize that adjacent probabilities are calculated in very similar ways. For example, in the game C=6,J=2

P(C4 is first J) = $q(6,2)q(5,2)q(4,2)p(3,2)$

P(C5 is first J) = $q(6,2)q(5,2)q(4,2)q(3,2)p(2,2)$

The product is the same up to the 3rd term and yet the old algorithm calculated each one from scratch each time. Instead of iterating over the teams, we can instead iterate over the cards, use some shortcuts to calculate P(Cv is first J), then add the result to a running total for the corresponding team.

When calculating P(Cv is first J), we can call the terms of the product with q’s the coefficient. The coefficient has the nice property that it grows by one term with each card:

P(C1 is first J) = $[1]\cdot p(6,2)$

P(C2 is first J) = $[q(6,2)]\cdot p(5,2)$

P(C3 is first J) = $[q(6,2)q(5,2)]\cdot p(4,2)$

So, by having a variable store the coefficient and multiplying the new value in each loop, we remove the redundancy found in the first algorithm.

The final algorithm looks something like this:

Create an array that stores win probabilities for each team
Create a variable that stores the coefficient
For each card v
1. coefficient*= $q(c-(v-1)+1,j)$
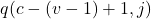
2. Calculate P(Cv is first J) = coefficient* $p(c-v+1,j)$
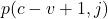
3. Add this value to the corresponding team win probability
Print the win probabilities for each team

If we count complexity in terms of number of times $p(c,j)$ is called, then the old algorithm has complexity $O(C^2)$ and the new one has a much better complexity $O(C)$ .

The new algorithm is faster in every case as well. Remember how for C=10000, J=1000, T=10 the old algorithm took 1333 milliseconds? Guess how long the new algorithm took. 400ms? 100ms?

The correct answer is 0ms! The algorithm was so fast that not a single millisecond of time was recognized. That’s C for ya.